Establishing valid causal inferences is difficult. It requires having realistic expectations about whether it is possible to establish a causal relationship from your research design. This is especially true for social science. According to Samii (2016), there has been an increased focus on causal empiricism in Political Science the last 15 years, as many theories form the late 1990s and early 2000s were based on evidence from simple OLS panel regressions, often producing biased results. These findings have come under scrutiny from findings using new methods such as quasi-experiments, natural experiments or other types of synthetic control (for example, IV Regression, Regression Discontinuity Design (RDD) or Differences in Differences (DID)). Central to these popularizing methods is the concepts of treatment effects and randomization.
ATE = Average Treatment Effect
Estimated by taking average of the differences between the value for treated units and the values for untreated units. We can never "know" the ATE, only estimate it (similarly for ATT & ATU).
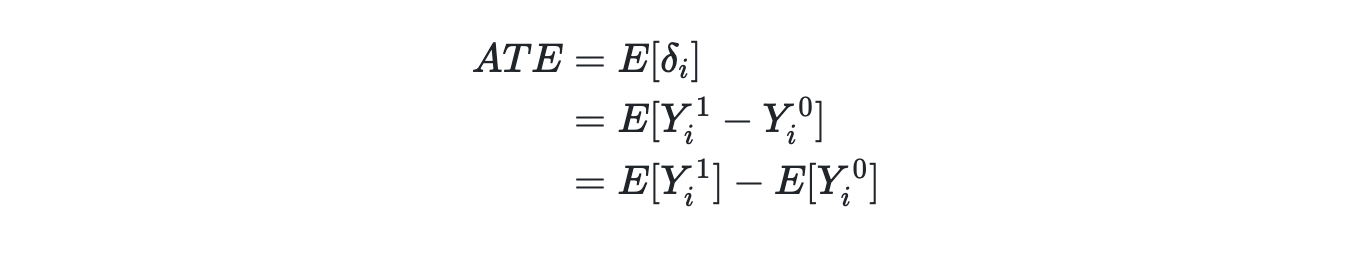
ATT = Average Treatment of the Treated
Estimated by taking the average effect for the treated group.
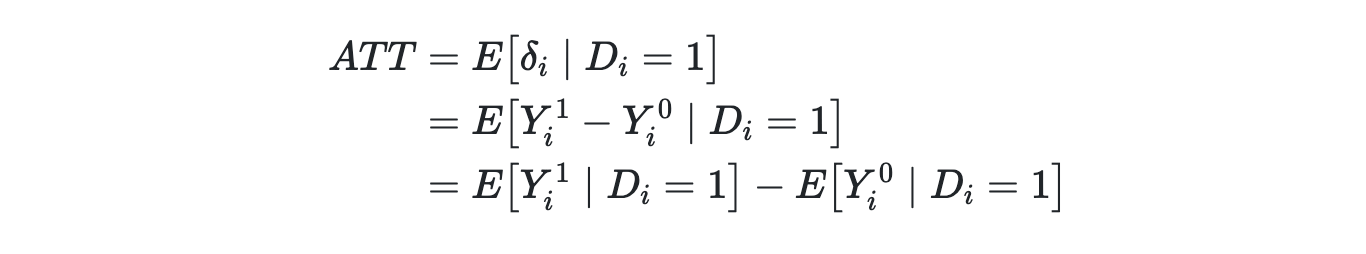
ATU = Average Treatment of the Untreated
Estimated by taking the average effect for the untreated group.
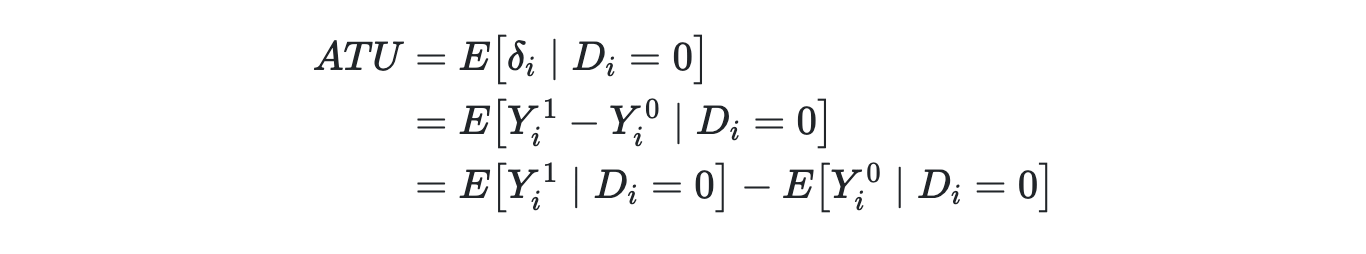
Independence assumption
To estimate unbiased effects, we rely on the independence assumption, meaning that our units we're selected independently of their potential outcomes, hence that they we're randomly selected. Y1 and Y0 are here assumed to be independent:
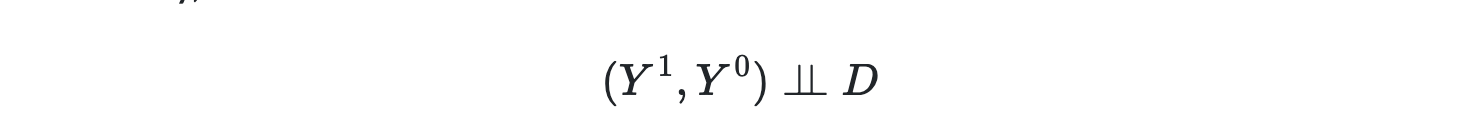
Fisher's Exact and Sharp Null
Roland A. Fisher (1925; 1935) proposed the explicit use of randomization in experimental design for causal inference. He devised a lady tasting tea randomized experiment to test the new design.
Fisher's exact test is a way to the exact probability value that the observed phenomenon was merely the product of chance, ie. the test produces a p-value. However, the fundamental problem of causal inference is still there: we never know a causal effect. We only can only estimate it.
Fisher's Sharp Null is a claim we make wherein no unit in our data, when treated, had a causal effect. The value of Fisher’s sharp null is that it allows us to make an “exact” inference that does not depend on hypothesized distributions (i.e., Gaussian) or large sample approximations.

